| Курсовая: Исследование операций
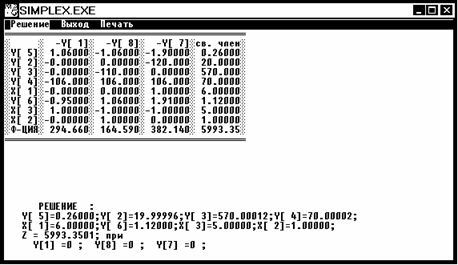
Вывод:
В результате решения я получил, что целочисленное оптимальное решение получается
в вершине 4, так как все значения x1=6, x2=1,x3
=5 в этой вершине целочисленные и Z5(5991)<Z4(5993),
следовательно получено оптимальное решение. Висящая вершина 5 и
прозондированные 1,2,3,4.
Плановые задания:
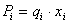 , где P – плановое
задание тыс. тонн, q – производительность состава, x – количество составов, i –
номер предприятия.
Для предприятия 1:
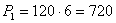 тыс. тонн;
Для предприятия 2:
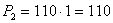 тыс. тонн;
Для предприятия 3:
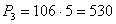 тыс. тонн.
Нелинейное программирование.
Задача математического программирования называется нелинейной, если нелинейны
ограничения или целевая функция.
Задачи нелинейного программирования бывают выпуклого и невыпуклого
программирования, с ограничениями и без ограничений, с квадратичными или
сепарабельными целевыми функциями. Задачи нелинейного программирования имеют
множество экстремальных точек, и сложность решения заключается в выделении
глобального оптимума, а не локального как это делается в большинстве
классических методов.
Разделяют задачи безусловной и условной оптимизации. Задачами безусловной
оптимизации называются задачи оптимизации функции многих переменных без
дополнительных ограничений. Существуют следующие методы безусловной
оптимизации: покоординатного спуска, градиентные, сопряженных направлений,
метод Ньютона. Задачами условной оптимизации называются задачи о оптимизации
целевой функции многих переменных f(x1, ., xn) при
условии, что эти переменные удовлетворяют следующим ограничениям:
qi(x1, ., xn) = 0, 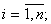
или
dj(x1, ., xn) 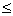 0, 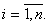
Решение задачи основывается на линейной или квадратичной аппроксимации целевой
функции для определения приращений x1, .,xn на каждой
итерации.
Существуют также приближенные методы решения нелинейных задач. Это методы
основанные на методе кусочно-линейной аппроксимации. Точность нахождения
решений зависит от количества интервалов, на которых мы находим решение
линейной задачи, максимально приближенной к нелинейной. Такой метод позволяет
производить расчеты с помощью симплекс-метода. Обычно в линейных моделях
коэффициенты целевой функции постоянны и не зависят от значения переменных.
Однако существует ряд задач, где затраты зависят от объема нелинейно. Такие
задачи решаются следующим способом: решают задачу ЛП с коэффициентами целевой
функции при максимальных значениях переменных. Если в решении мы получили
переменные, для которых брались коэффициенты, значит задача решена. В
противном случае мы изменяем коэффициенты при целевой функции на коэффициенты
при вновь полученных значениях переменных и решаем полученную задачу ЛП. Так
мы повторяем до тех пор, пока не будет получено на двух последующих шагах
одно и то же решение.
Решение задачи нелинейного программирования.
Метод кусочно – линейной аппроксимации.
В нашей задаче есть такая величина, как коэффициент увеличения затрат при
нагрузке, который не использовался нами при решении задачи методами ЛП и ЦЛП.
Собственно этот коэффициент и введен для превращения задачи в нелинейную
путем нелинейной зависимости между увеличением затрат и загрузкой
предприятий.
Составим таблицу:
| № предприятия | Коэффи- Циент затрат % | Количе-ство составов | Коэфф. измене-ния затрат | Затраты на 1т у.е. | Доход | Прибыль На 1т у.е. | Прибыль на 1 состав у.е. | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | Œ | 100 | 6,17 | 1 | 6 | 11,64 | 5,64 | 676,8 | | 70 – 100 | 4.31–6,16 | 1,4 | 8,4 | 3,24 | 388,8 | | 50 – 70 | 3,08–4,31 | 1,6 | 9,6 | 2,04 | 244,8 | | 30 – 50 | 1,85–3,08 | 1,7 | 10,2 | 1,44 | 172,8 | | до 30 | до 1,85 | 1,8 | 10,8 | 0,84 | 100,8 | | | 100 | 6,18 | 1 | 7 | 11,175 | 4,175 | 459,25 | | 70 – 100 | 4,33-6,18 | 1,2 | 8,4 | 2,775 | 305,25 | | 50 – 70 | 3,09-4,33 | 1,4 | 9,8 | 1,375 | 151,25 | | 30 – 50 | 1,85-3,09 | 1,5 | 10,5 | 0,675 | 74,25 | | до 30 | до 1,85 | 1,7 | 11,9 | - 0,725 | - 79,75 | | Ž | 100 | 5,66 | 1 | 8 | 10,78 | 2,78 | 294,66 | | 70 – 100 | 3,96-5,66 | 1,3 | 10,4 | 0,38 | 40,28 | | 50 – 70 | 2,83-3,96 | 1,6 | 12,8 | - 2,02 | - 214,12 | | 30 – 50 | 1,7 – 2,83 | 1,7 | 13,6 | - 2,82 | - 298,92 | | до 30 | до 1,7 | 1,9 | 15,2 | - 4,42 | - 458,52 |
Где доход (Д) рассчитывается по формуле:
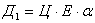 , где
Ц – цена готовой продукции, Е – извлечение, a - содержание полезного компонента.
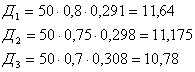
Прибыль (П) рассчитывается по формуле:
П = Д – З , где Д – доход, З – затраты.
Затраты (З) рассчитываются по формуле:
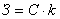 , где С –
затраты на добычу, транспортировку и переработку, 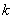
- коэффициент изменения затрат.
1. Пусть x1, x2, x3 принимают свои максимальные значения, тогда
Z1 = 676,8x1 + 459,25x2 + 294,66x3  MAX
Ограничения:
x1 + x2 + x3 =12 – по количеству составов;
x1 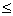 6,17 - максимальный объем добычи руды с предприятия 1;
x2 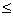 6,18 - максимальный объем добычи руды с предприятия 2;
x3 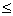 5,66 - максимальный объем добычи руды с предприятия 3;
0,96x1 + 0,11x2 – 0,95x3 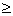
0 – по максимально допустимому содержанию полезного компонента в руде;
-0,84x1 + 1,06x3 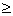 0 – по минимально допустимому содержанию
полезного компонента в руде.
Решение 1.
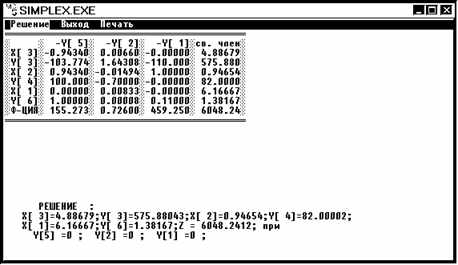
x1 = 6,17 x2 = 0,95 x3=4,88 Z1 = 6048,24
2. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z2 будет равен 676, 8.
Так как x2=0,95; x2 < 1,87, то коэффициент при x2
в целевой функции Z2 будет равнятся -79,75.
Так как x3=4,88; 3,96 < 4,88 <5,66, следовательно x3
попадает в интервал 3,96 – 5,66, следовательно коэффициент при x3 в
целевой функции Z2 будет равен 40,28.
Следовательно Z2 = 676,8x1 – 79,75x2 + 40,28x3
Решение 2.
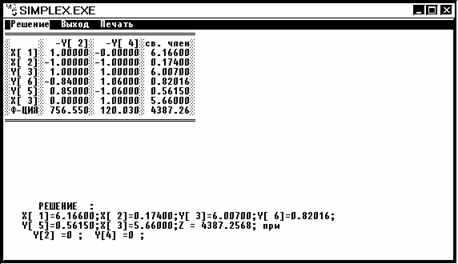
x1 = 6,17 x2 = 0,17 x3 = 5,66 Z2 = 4387,26
3. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z3 будет равен 676, 8.
Так как x2=0,17; x2 < 1,87, то коэффициент при x2
в целевой функции Z3 будет равнятся -79,75.
Так как x3=5,66 – максимально возможный, то коэффициент при x3 в
целевой функции Z3 будет равен 294,68.
Следовательно Z3 = 676,8x1 – 79,75x2 + 294,68x3
Решение 3.
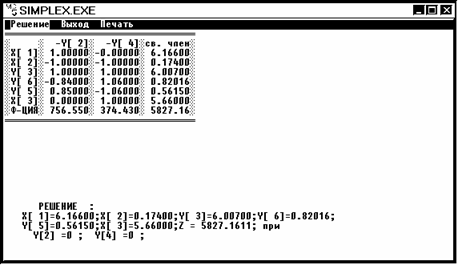
x1 = 6,166 x2 = 0,17 x3 = 5,66 Z3 = 5827,16
Вывод:
Так как на третьем шаге мы получили значения переменных равных значениям
переменных на втором шаге, то мы получили искомое решение задачи нелинейного
программирования. Третий шаг, за счет того, что значения коэффициента при x
3 были увеличены с 40,28 до 294,68, улучшил целевую функцию Z3
на 5827,16 – 4387,26 = 1439,9 у.е.
Плановые задания предприятиям.
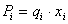 , где P – плановое
задание тыс. тонн, q – производительность состава, x – количество составов, i –
номер предприятия.
Для предприятия 1:
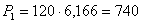 тыс. тонн;
Для предприятия 2:
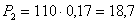 тыс. тонн;
Для предприятия 3:
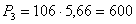 тыс. тонн.
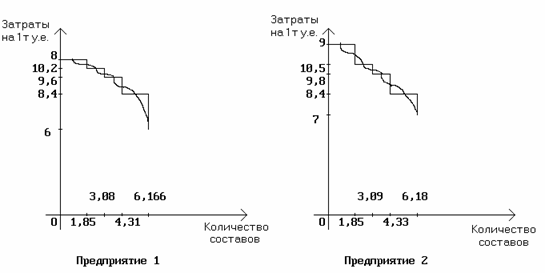
Аппроксимация кривой зависимости затрат от количества составов. Примеры
графиков для предприятий 1 и 2.
Динамическое программирование. (ДП)
Динамическими называются задачи экономики, организации и управления, в
которых необходимо распределять ресурсы на каждом этапе какого – либо
промежутка (времени). Формулировка задачи ДП:
Имеется некая система S, находящаяся в первоначальном состоянии S. Данная
система имеет какие – либо параметры. При переходе системы из одной точки в
другую необходимо в каждый момент времени выбирать направление дальнейшего
движения из нескольких допустимых направлений при условии, что каждому
направлению соответствует своя эффективность (параметры системы изменяются по
разному), и необходимо таким образом спланировать маршрут из начальной точки в
конечную, чтобы критерий эффективности достигал экстремального значения.
Иными словами из множества допустимых управлений U=(U1, U2
, ., Un) необходимо найти оптимальное, при котором система переходит
из своего начального состояния в конечное таким образом, что критерий
оптимальности W достигает своего максимума.
Динамическое программирование представляет собой метод оптимизации
многошаговых процессов по шагам. Локальный оптимум на каждом шаге должен
рассчитываться не как оптимальный на данном этапе, а как дающий максимальное
значение критерия оптимальности в конце движения. Несоблюдение этого правила
приводит к серьезным ошибкам, поэтому при решении задач ДП двигаются обычно
из конца пути в начало, рассчитывая затраты при движении в каждом
направлении, а затем из начала в конец, находя локальный оптимум из
рассчитанных затрат на каждом шаге. Таким образом получаем максимальное
значение критерия оптимальности.
В основе расчетов методом динамического программирования лежит принцип
Беллмана. Он звучит:
оптимальное управление обладает тем свойством, что какавы бы ни были
достигнутые состояния и решения до данного момента, последующее решение должно
составлять оптимальное поведение относительно состояния, достигнутого на данный
момент.
Решение задачи динамического программирования.
Распределение ресурсов предприятиям.
Данные возьмем из задачи нелинейного программирования: количество составов и
прибыль на 1 состав для каждого предприятия:
Предприятие 1.
| Количество составов | Прибыль на 1 состав | | 6,17 | 676,8 | | 4,31 – 6,17 | 388,8 | | 3,08 – 4,31 | 244,8 | | 1,85 – 3,08 | 172,8 | | до 1,85 | 100,8 |
Предприятие 2.
| Количество составов | Прибыль на 1 состав | | 6,18 | 459,25 | | 4,33 – 6,18 | 305,25 | | 3,09 – 4,33 | 151,25 | | 1,85 – 3,09 | 74,25 | | до 1,85 | -78,75 |
Предприятие 3.
| Количество составов | Прибыль на 1 состав | | 5,66 | 294,68 | | 3,96 – 5,66 | 40,28 | | 2,83 – 3,96 | -214,12 | | 1,7 – 2,83 | -298,92 | | до 1,7 | -458,52 |
Количество составов,выделенных всем трем предприятиям (N), равно 14.
Рассчитаем эффективность использования средств предприятиями. Для этого
прибыль на один состав умножим на количество составов, при которых
достигается эта прибыль на каждом из предприятий.
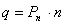 , где n – количество составов, Pn – прибыль при этом количестве составов.
| Количество составов | Предприятие 1 | Предприятие 2 | Предприятие 3 | | 1 | 100,8 | -78,15 | -458,52 | | 2 | 345,6 | 148,5 | -597,94 | | 3 | 518,4 | 222,75 | -642,36 | | 4 | 979,2 | 605 | 161,12 | | 5 | 1944 | 1526,25 | 201,40 | | 6 | 2332,8 | 1831,5 | 1768,08 |
Рассчитаем 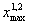 -
максимально возможное количество составов для предприятий 1 и 2. 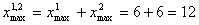
составов. Теперь рассчитаем минимально возможное количество составов для
предприятий 1 и 2, исходя из того, что максимально возможное количество
составов для предприятия 3 равно 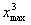
= 6 составов, тогда 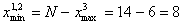
составов. Составим таблицу выделения средств двум предприятиям (1 и 2). Здесь x
- общее количество ресурсов (составов) для двух предприятий; x = x1
+ x2; 0 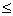 x
1 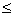 6 –
допустимое количество составов для предприятия 1; 0 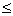
x2 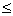 6 –
допустимое количество составов для предприятия 2. Отсюда видно, что 0 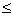
x 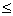 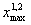
, однако количество составов для предприятия 3 не может превышать 6,
следовательно x 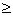 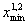
, следовательно 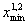 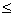
x 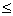 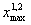
; 8 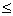 x 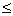
12. q1, q2 – эффективность использования средств
предприятиями 1 и 2 соответственно взятая из предыдущей таблицы. W2
= q1 + q2 – суммарная эффективность обоих предприятий. 
Наибольшую суммарную эффективность для каждого значения x будем подчеркивать.
| x | x1 | X2 | Эффективность | q1 | q2 | W2 | | 8 | 2 | 6 | 345,6 | 1831,5 | 2177,1 | | 3 | 5 | 518,4 | 1526,25 | 2044,65 | | 4 | 4 | 979,2 | 605 | 1584,2 | | 5 | 3 | 1944 | 222,75 | 2166,75 | | 6 | 2 | 2332,8 | 148,5 | 2481,3 | | 9 | 3 | 6 | 518,4 | 1831,5 | 2349,9 | | 4 | 5 | 979,2 | 1526,25 | 2505,45 | | 5 | 4 | 1944 | 605 | 2549 | | 6 | 3 | 2332,8 | 222,75 | 2555,55 | | 10 | 4 | 6 | 979,2 | 1831,5 | 2810,7 | | 5 | 5 | 1944 | 1526,25 | 3470,25 | | 6 | 4 | 2332,8 | 605 | 2937,8 | | 11 | 5 | 6 | 1944 | 1831,5 | 3775,5 | | 6 | 5 | 2332,8 | 1526,25 | 3859,05 | | 12 | 6 | 6 | 2332,8 | 1831,5 | 4164,3 |
Теперь составим таблицу выделения средств всем трем предприятиям. Так как N –
общее количество составов равно 14, а максимально возможное количество составов
для предприятий 1 и 2 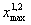
=12, то всем трем предприятиям может быть выделено 13 или 14 составов. W3
– суммарная эффективность всех трех предприятий.
Количество Составов | x3 | x | Эффективность использования ресурсов | q3 | W2 | W3 | | 13 | 1 | 12 | -458,52 | 4164,3 | 3705,78 | | 2 | 11 | -597,94 | 3859,05 | 3261,11 | | 3 | 10 | -642,36 | 3470,25 | 2827,89 | | 4 | 9 | 161,12 | 2555,55 | 2716,67 | | 5 | 8 | 201,4 | 2481,3 | 2682,7 | | 14 | 2 | 12 | -597,94 | 4161,3 | 3563,36 | | 3 | 11 | -642,36 | 3859,05 | 3216,69 | | 4 | 10 | 161,12 | 3470,25 | 3631,12 | | 5 | 9 | 201,4 | 2555,55 | 2756,95 | | 6 | 8 | 1768,08 | 2481,3 | 4249,38 |
W3 максимальное равно 4249,38, следовательно Z = 4249,38.
x3 = 6; x2 = 2; x3 = 6.
Вывод:
В результате решения задачи динамического программирования я получил, что
максимальное значение целевой функции Z = 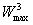
= 4249,38 получается при количестве составов, выделенных 3 предприятиям N = 14,
и количестве составов выделенных предприятию 3 x3 = 6. При этом
количество составов для предприятий 1 и 2 равно 8. Максимальная эффективности
использования 8 составов предприятиями 1 и 2 достигается при выделении
предприятию 1 - 6 составов, а предприятию 2 – 2 состава, и она равна 2481,3.
Следовательно x1 = 6, x2 = 2, x3 = 6, Z =
4249,38.
Плановые задания предприятиям:
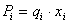 , где P – плановое
задание тыс. тонн, q – производительность состава, x – количество составов, i –
номер предприятия.
Для предприятия 1:
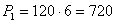 тыс. тонн;
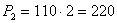 тыс. тонн;
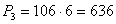 тыс. тонн.
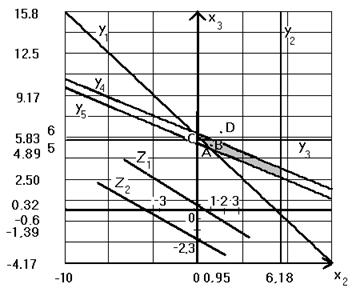
Графическая интерпретация решений.
1. Решение задачи ЛП.
Из ограничения 1 задачи ЛП:
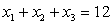
Выразим
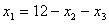
Ограничения:
1) x1 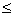 6,17 , значит 12 - x2 - x3 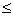 6,17;
x2 + x3 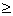 5,84
y1 = x2 + x3 = 5,84
x3 = 5,84 – x2;
2) x2 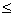 6,18
y2 = x2 = 6,18;
3) x3 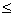 5,66
y3 = x3 = 5,66;
4) 0,96 x1 + 0,12 x2 – 0,95 x3 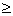 0
0,96 (12 – x2 – x3) + 0,12 x2 – 0,95 x3 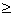 0
-0,84 x2 – 1,9 x3 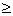 11,52
0,84 x2 + 1,9 x3 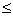 11,52
y4 = 0,84 x2 + 1,9 x3 = 11,52
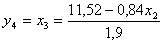 ;
5) –0,84 x1 + 1,06 x3 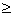 0
-0,84 (12 – x2 – x3) + 1,06 x3 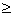 0
0,84 x2 + 0,84 x3 + 1,06 x3 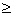 10,08
0,84 x2 + 1,9 x3 = 10,08
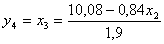 ;
Целевая функция:
Z = 676,8 (12 – x2 – x3) + 459,25 x2 + 294,66 x
3 = 8121,6 – 217,55 x2 – 382,14 x3;
Рассмотрим, что происходит с графиком целевой функции при ее увеличении:
1) Z1 = 8000
8121,6 – 217,55 x2 – 382,14 x3 = 8000
-217,55 x2 – 382,14 x3 = 8000 – 8121,6
217,55 x2 + 382,14 x3 =121,6
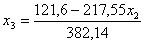 ;
2) Z2 = 9000
-217,55 x2 – 382,14 x3 = 9000 – 8121,6
217,55 x2 + 382,14 x3 = – 878,4
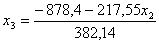
Мы получили, что график функции Z2 расположен ниже чем график функции
Z1. Однако Z2 > Z1 (9000 > 8000).
Следовательно своего максимального значения целевая функция достигает в самой
нижней точке области относительно целевой функции (в той точке, через которую
график целевой функции будет проходить первым при уменьшении целевой функции).
Обозначим эту точку на графике A. Координаты точки A (0,95;4,89). x2
= 0,95; x3 = 4,89, что соответствует решению с помощью симплекс –
метода.
2. Задача ЦЛП.
Максимального значения целевая функция задачи ЦЛП достигает при x2 =
1, x3 = 5. На графике решение задачи ЦЛП – точка B с координатами
(1;5).
3. Задача нелинейного программирования.
x2 = 0,17, x3 = 5,66. На графике точка C с координатами (0,17;5,66).
4. Задача ДП.
x2 = 2, x3 = 6. На графике точка D с координатами (2;6).
Трудоемкость и эффективность решения модели различными методами.
 Метод Метод
Свойство | ЛП | ЦЛП | Нелинейное | ДП | Использование Симплекс – метода и ПК | Небольшое (1 проход) | Большое (много проходов) | Большое (много проходов) | НЕТ | | Размер расчетов без ПК | Низкий (только расчет плановых заданий) | Низкий (только расчет плановых заданий) | Средний (расчет дохода, прибыли, затрат, плановых заданий) | Большой (все расчеты производятся вручную) | | Размер подготовительных и промежуточных расчетов | Низкий (только ограничения) | Средний (ограничения ЛП + ветвление) | Высокий (ограничения ЛП + составление таблицы + промежуточ-ные подстановки коэффициен-тов) | Очень большой | | Общее время решения | Низкое | Среднее | Среднее | Высокое | | Чувствитель-ность к ограничениям по содержанию полезного компонента в руде | Есть | Есть | Есть | Нет | | Использование коэффициента увеличения затрат при нагрузке | Нет | Нет | Есть | Есть | | Размер целевой функции | Максимальный 6048,2412 | Средний 5993,3501 | Средний 5827,1611 | Низкий 4249,38 | | Общая эффективность и приближенность условий к реальным | Низкая (не учитывается коэффициент изменения затрат и целочислен- ность решения) | Средняя (не учитывается коэффициент изменения затрат) | Средняя (не учитывается целочислен-ность решения) | Средняя (низкая прибыль) | | | | | | |
О проекте.
Проект выполнен студентом второго курса факультета РПМ Московского
государственного горного университета Солодовниковым Дмитрием.
Использованная литература:
· Резниченко С.С., Ашихмин А.А. Математические методы и моделирование
в горной промышленности. – М.: Издательство Московского горного университета,
1997, 404 c.
Страницы: 1, 2
|
ИНТЕРЕСНОЕ
|

 Вывод:
В результате решения я получил, что целочисленное оптимальное решение получается
в вершине 4, так как все значения x1=6, x2=1,x3
=5 в этой вершине целочисленные и Z5(5991)<Z4(5993),
следовательно получено оптимальное решение. Висящая вершина 5 и
прозондированные 1,2,3,4.
Плановые задания:
Вывод:
В результате решения я получил, что целочисленное оптимальное решение получается
в вершине 4, так как все значения x1=6, x2=1,x3
=5 в этой вершине целочисленные и Z5(5991)<Z4(5993),
следовательно получено оптимальное решение. Висящая вершина 5 и
прозондированные 1,2,3,4.
Плановые задания:
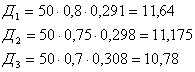 Прибыль (П) рассчитывается по формуле:
П = Д – З , где Д – доход, З – затраты.
Затраты (З) рассчитываются по формуле:
Прибыль (П) рассчитывается по формуле:
П = Д – З , где Д – доход, З – затраты.
Затраты (З) рассчитываются по формуле:
 x1 = 6,17 x2 = 0,95 x3=4,88 Z1 = 6048,24
2. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z2 будет равен 676, 8.
Так как x2=0,95; x2 < 1,87, то коэффициент при x2
в целевой функции Z2 будет равнятся -79,75.
Так как x3=4,88; 3,96 < 4,88 <5,66, следовательно x3
попадает в интервал 3,96 – 5,66, следовательно коэффициент при x3 в
целевой функции Z2 будет равен 40,28.
Следовательно Z2 = 676,8x1 – 79,75x2 + 40,28x3
Решение 2.
x1 = 6,17 x2 = 0,95 x3=4,88 Z1 = 6048,24
2. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z2 будет равен 676, 8.
Так как x2=0,95; x2 < 1,87, то коэффициент при x2
в целевой функции Z2 будет равнятся -79,75.
Так как x3=4,88; 3,96 < 4,88 <5,66, следовательно x3
попадает в интервал 3,96 – 5,66, следовательно коэффициент при x3 в
целевой функции Z2 будет равен 40,28.
Следовательно Z2 = 676,8x1 – 79,75x2 + 40,28x3
Решение 2.
 x1 = 6,17 x2 = 0,17 x3 = 5,66 Z2 = 4387,26
3. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z3 будет равен 676, 8.
Так как x2=0,17; x2 < 1,87, то коэффициент при x2
в целевой функции Z3 будет равнятся -79,75.
Так как x3=5,66 – максимально возможный, то коэффициент при x3 в
целевой функции Z3 будет равен 294,68.
Следовательно Z3 = 676,8x1 – 79,75x2 + 294,68x3
Решение 3.
x1 = 6,17 x2 = 0,17 x3 = 5,66 Z2 = 4387,26
3. Так как x1=6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z3 будет равен 676, 8.
Так как x2=0,17; x2 < 1,87, то коэффициент при x2
в целевой функции Z3 будет равнятся -79,75.
Так как x3=5,66 – максимально возможный, то коэффициент при x3 в
целевой функции Z3 будет равен 294,68.
Следовательно Z3 = 676,8x1 – 79,75x2 + 294,68x3
Решение 3.
 x1 = 6,166 x2 = 0,17 x3 = 5,66 Z3 = 5827,16
Вывод:
Так как на третьем шаге мы получили значения переменных равных значениям
переменных на втором шаге, то мы получили искомое решение задачи нелинейного
программирования. Третий шаг, за счет того, что значения коэффициента при x
3 были увеличены с 40,28 до 294,68, улучшил целевую функцию Z3
на 5827,16 – 4387,26 = 1439,9 у.е.
Плановые задания предприятиям.
x1 = 6,166 x2 = 0,17 x3 = 5,66 Z3 = 5827,16
Вывод:
Так как на третьем шаге мы получили значения переменных равных значениям
переменных на втором шаге, то мы получили искомое решение задачи нелинейного
программирования. Третий шаг, за счет того, что значения коэффициента при x
3 были увеличены с 40,28 до 294,68, улучшил целевую функцию Z3
на 5827,16 – 4387,26 = 1439,9 у.е.
Плановые задания предприятиям.
 Аппроксимация кривой зависимости затрат от количества составов. Примеры
графиков для предприятий 1 и 2.
Аппроксимация кривой зависимости затрат от количества составов. Примеры
графиков для предприятий 1 и 2.
 Метод
Метод