Диплом: Оценка имущества

оставить до наступления следующей даты. В каждый последующий период ставка

процентов возрастает.

Ставка процента по облигациям может быть плавающей, т.е. изме­няющейся

регулярно (каждые полгода и т.п.) в соответствии с динами­кой ставки

рефинансирования Центрального Банка или уровнем доходно­сти государственных

ценных бумаг, размещаемых путем аукционной про­дажи.

В отдельных странах в качестве антиинфляционной меры практику­ет выпуск

облигаций с номиналом, индексируемым с учетом роста индек­са потребительских

цен.

По некоторым облигациям проценты не выплачиваются. Их владель­цы получают

доход благодаря тому, что покупают эти облигации с ди­сконтом (скидкой против

нарицательной стоимости), а погашают - по номиналу.

Доход по облигациям может выплачиваться в форме выигрышей, получаемых

отдельными их владельцами по итогам регулярно проводимых тиражей.

Облигации, являясь объектом купли-продажи на рынке ценных бумаг, имеют

рыночную цену, которая в момент эмиссии может быть равна номиналу, а также

быть ниже или выше его. Рыночные цены существенно различаются между собой,

поэтому для достижения их сопоставимости рассчитывается курс облигации. Под

курсом облигации понимают покупную цену одной облигации в расчете на 100

денежных единиц номинала. Курс облигации зависит от средней величины ссудного

процента на рын­ке капиталов, существующего в данный момент, срока погашения,

степе­ни надежности эмитента и ряда других факторов.

Расчет курса производится по формуле:

(2.21)

где Рк - курс облигации;

Р - рыночная цена;

N - номинальная цена облигации.

Доходность облигаций характеризуется рядом параметров, которые зависят от

условий, предложенных эмитентом. Так например, для облигаций, погашенных в

конце срока, на которые они выпущены, доходность измеряется купонной

доходностью, текущей доходностью и полной доход­ностью.

Купонная доходность - норма процента, которая указана на цен­ной бумаге и

которую эмитент обязуется уплатить по каждому купону. Платежи по купонам

могут производиться раз в квартал, по полугоди­ям или раз в год.

Например, на облигации указана купонная доходность в 11,75 % годовых.

Номинал облигации 100 тыс. руб. На каждый год имеется два купона. Это значит,

что облигация принесет полугодовую прибыль 5,875 тыс. руб. (100 *0.1175 *

0,50), а за год 11.75 тыс. руб.

Текущая доходность характеризует выплачиваемый годовой процент на вложенный

капитал, т.е. на сумму, уплаченную в момент приобрете­ния облигации. Текущая

доходность определяется по формуле:

(2.22)

где норма доходности по купонам;

N - номинальная цена облигации;

Р - рыночная цена (цена приобретения).

Например, если купонная доходность

=11,75 %, а курс облига­ции 95,0, то текущая доходность составит

Вместе с тем текущая доходность не учитывает изменения цены об­лигации за

время ее хранения, т.е. другого источника дохода.

Полная доходность учитывает все источники дохода. Показатель полной

доходности измеряют процентной ставкой, называемой ставкой помещения.

Начисление процентов по ставке помещения на цену приобре­тения дает доход,

эквивалентный фактически получаемому по ней дохо­ду за вес! период обращения

этой облигации до момента ее погашения. Ставка помещения является расчетной

величиной и в явном виде на рын­ке ценных бумаг не выступает.

Стоимость облигации равна сумме двух слагаемых - современной стоимости ее

аннуитетов (приведенной сумме ежегодных выплат процент­ных платежей) и

современной стоимости ее номинала:

P = N g an/i + N (1+i)-n = N (gan/i + (1+i)-n) (2.23)

Если использовать 2.1, то

P = (gan/i + (1+i)-n) * 100

где Р - рыночная цена облигации;

Рк – курс облигации;

N - номинал облигации;

g- купонная ставка;

n- время от момента приобретения до момента погашения обли­гации;

i - ссудный процент, предлагаемый банками в момент продажи облигации.

Пример 2.3. По облигации номинальной стоимостью в 100 тыс.руб. в течение 10 лет

(срок до ее погашения) будут выплачиваться ежегод­но в конце года процентные

платежи в сумме 10 тыс.руб. (

= 10 %), которые могут быть помещены в банк под 11 % годовых.

Рыночная цена облигации по (2.25) составит:

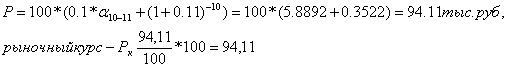
В данном случае облигация продается с дисконтом (ниже номинала), т.к.

= 10 % <i = 11 %, Рк = 100.

Предположим далее, что ставка банковского процента снизилась с 11 % до

9,5 %. Номинальная стоимость облигации и размер ежегодных выплат при

этом сохраняется неизменным. Тогда рыночная цена облига­ции составит:

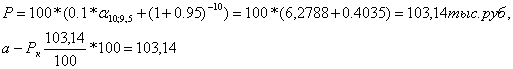
В этом случае облигация продается с премией, т.к. . = 10 % > i' = 9,5 %, a P>100.

Так как цена облигации при ее продаже эквивалентна будущим по­ступлениям от

нее, то при приближении момента ее выкупа курс обли­гации, купленной с

премией, понижается. Обусловлено это тем, что по всей уже выплачена большая

часть доходов и к моменту выкупа остается получить только ее номинальную

стоимость. Курс же облигации, куплен­ной с дисконтом, будет повышаться, так

как в момент ее погашения владелец получит сумму, равную номиналу (приобрел

же он ее по пониженной цене).

Таким образом, с приближением даты выкупа происходит погашение дисконта.

Погашенный дисконт увеличивает оценку облигации и ее курс.

Для получения показателя, дающего количественную характеристику зависимости

цены облигации от купонного дохода и рыночной процент­ной ставки,обозначим:

N(1 + i)-n= Q - современная стоимость номинала облигации.

Разность между продажной и выкупной ценой облигации (номина­лом облигации) равна

Е = Р -N

Сделав ряд преобразований, определим эту разность, как

E = g-i/i *Nan/i (2.25)

При g=i, Е=0, т.е. облигация продается по номиналу.

При g>i, Е - величина положительная и облигация продает­ся с премией.

При g<i, Е < 0 и облигация продается с дисконтом.

Ранее мы рассматривали понятие - ставка помещения. Естественно, что любой

инвестор, планирующий сделать инвести­ции в облигации, должен рассчитать

ставку помещения.

Для приближенной оценки ставки помещения соотносят годовой до­ход от

облигации со средней ее ценой. Средняя цена определяется на основе номинала и

цены покупки. Для облигаций, приобретенных с дис­контом, ставка помещения

равна:

I = (gN + (N-P)/n): (P+N)/2 (2.26)

а для облигаций, купленных с премией:

I = (gN + (N-P)/n): (P+N)/2 (2.27)

где n - числи лет, оставшихся до погашения;

g - годовой купонный доход;

P- цена приобретения;

N - номинал облигаций.

По данным примера 5.5 рассчитаем ставку помещения для случая продажи

облигации с дисконтом:

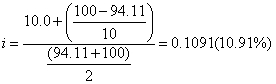
Приведем ряд расчетных формул показателей доходности для дру­гих видов

облигаций.

Облигации без выплаты процентов. Для данного вида облигаций доходом

является разность между ценой погашения (номиналом) и ценой приобретения. В

этом случае показатель доходности равен

(2.28)

где Pk - курс облигации, Р„ ^ 100;

n - срок от момента приобретения до момента выкупа.

Облигации с выплатой процентов в конце срока обращения. Владе­лец данного

вида облигаций в конце срока обращения получит ее номи­нальную стоимость с

начисленными процентами. Показатель доходности:

I = (100 : Pk)1/n (1+g) – 1 (2.29)

где g - проценты, начисляемые на номинал.

Пример 2.4. Банк выпустил облигации со сроком погашения через 10 лет. Начисление

процентов на номинал – 6 % годовых. Выплата про­центов и номинальная

стоимость выплачивается при погашении. Опреде­лить доходность облигации (ставку

помещения), если ее курс при пер­воначальной реализации составил: а) 108,0; б)

92,0:

а) 5.19 %

б)6,89 %

2.5. Дополнительные характеристики облигаций.

Доходность является важнейшим, но не единственным критерием выбора облигаций.

Другим показателем привлекательности для инвесто­ра того или иного вида

облигации является продолжительность срока до ее погашения. При увеличении

последнего растет степень финансового риска для ее владельца. Безусловно,

риск приобретения облигаций с купонными доходами значительно ниже риска,

связанного с облигаци­ями, выплата процентов, по которым производится в конце

срока. В свя­зи с этим существует ряд показателей, которые характеризуют в

той или иной степени особенности распределения доходов в период времени от

момента покупки облигации до момента погашения.

Одним из таких показателей является средний срок облигации. При ежегодных

купонных выплатах средний срок выплат определяется как:

Т = h * (g (1+h):2 + 1) : gh + 1 (2.30)

где h - сроки платежей по купонам в годах;

g - купонный процент.

Пример 2.5.Облигация номиналом 10000 руб. выпущена со сроком погашения через 4

года. Ежегодно по купонам выплачивается 12 % от номинала. Определить

средний срок облигации

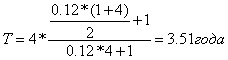
Наряда с показателей среднего срока облигации существует близ­кий ему по

экономическому смыслу показатель, характеризующий сред­нюю продолжительность

платежей. Иногда его называют показателем из­менчивости; обозначим его

символом.

Данный показатель является средней величиной.

В случае, когда проценты по облигациям выплачиваются ежегодно, расчет средней

продолжительности платежей производится по формуле;

D = S tj *Sj Vt : S Sj V (2.31)

Пример 2.6. Облигация выпущена сроком на 4 года, номиналом 1000 руб. Ежегодно

выплачиваются по купонам 12 % годовых, рыночная процентная ставка -

12,5 %. Рыночная цена облигации 985 руб.

Определить показатель продолжительности платежей.

Рассчитаем все элементы, входящие в (2.31)

t	Vt	Sj	SjVt	t SjVt
1	0.8889	120	106.668	106.668
2	0.7901	120	94.815	189.630
3	0.7023	120	84.280	252.840
4	0.6243	120+1000	692.973	3345.980

D = 3345,980 : 985,0 = 3,4 года.

Приведенные формулы для расчета величин Т и Д показывают, что величина Т

не зависит от рыночной процентной ставки (ссудного про­цента), в то же время

величина Д зависит от ее изменения: с ростом ссудного процента его

влияние на отдаленные по времени платежи пада­ет, что, в свою очередь, снижает

величину Д.

Поэтому основным назначением показателя Д является определение

эластичности цены по процентной ставке, т.е. измерение степени колеблемости

цены облигации при незначительных изменениях величины процентной ставки на

денежном рынке.

Решение этой задачи осуществляется с помощью модифицированной величины Д,

которая в отечественных экономических публикациях по­лучила название

модифицированной изменчивости (МД).

МД = Д/ (1+i:p) (2.32)

Где Д - средняя продолжительность платежей;

i - рыночная процентная ставка;

Р - число выплат процентов в году.

Изменение цены облигации в результате изменения процентной ставки

определяется по формуле:

▲P = - 0.01*МД * ▲ i * P (2.33)

где ▲P - изменение цены облигации;

▲ i - изменение рыночной процентной ставки.

Пример 2.7. По данным примера 2.4 рассчитаем показатель моди­фицированной

изменчивости

Определим, как изменится цена облигации, если рыночная процент­ная ставка

возрастет с 12,5 % до 12,8 %.

▲Р= -0001*3,0222*0,3*985=-8,9306.

Откуда ожидаемое значение цены составит:

985,0 - 8,9306 = 976,0694.

Реакция цены облигации на значительные изменения рыночной про­центной ставки

измеряется с помощью показателя, получившего назва­ние выпуклость (Сx

).

Расчет производится по формуле

Сх= 1/(1+ i:p) * (M2 +Д2 + Д: Р) (2.34)

Где М2 - дисперсия показателей времени платежа;

значения остальных символов те же, что и в (2.11-2.12).

М2 = 1/Р S t2 Sj Vt – Д2 (2.35)

где Р - цена облигации.

Сдвиг в цене облигации в результате значительного изменения рыночных

процентных ставок определяется как

▲P = - РМД * ▲ i: 100 +( (0.5P * Cx▲ i) : 10000) (2.36)

Пример 2.8. Рассмотрим возможность изменения цены облигации, если рыночная

процентная ставка возросла с 12,5 % до 15,0 %, осталь­ные

условия аналогичны примерам 2.4 и 2.5.

t	t2	Vt	Sj	t2 SjVt
1	1	0.8889	120	106.668
2	4	0.7901	120	189.630
3	9	0.7023	120	252.840
4	16	0.6243	120+1000	11187.360
Итого				12431,808

М2 = 1,0611

Рассчитаем Сх:

Так как ▲i = 15- 12,5 = 2,5 %, то по (2.15) находим

▲Р= - 985,0 * 3,0222 * (15 - 12,5 / 100) + (0,5 * 985,0 * 14,2410 * 2,5

2) / 1000= - 70,038

т.е. рост процентной ставки на 2,5 % вызывает снижение цены облигации до

уровня 985,0 + (-70,038) = 914,962 руб.

2.6. Анализ доходности портфеля облигаций.

Набор ценных бумаг, находящихся в распоряжении инвестора, называется

портфелем ценны бумаг.

Рассмотрим некоторые методы оценки портфеля облигаций. Простейший анализ

портфеля облигаций заключается в оценке его полной доход­ности и среднего

показателя изменчивости. Более сложный анализ свя­зан с выбором структуры

портфеля, т.е. должен содержать рекомендации относительно того, какую долю

капитала целесообразно вложить в тот или иной вид из циркулирующих на рынке

ценных бумаг.

Годовая ставка сложных процентов, получаемых от облигаций, со­ставляющих

портфельные инвестиции, может служить показателем доходности портфеля. Одним из

методов определения величины этой ставки является решение уравнения, в котором

общая стоимость облигаций по цене приобретения (

) приравнивается к сумме современных величин всех платежей (

). Отсюда, уравнение имеет вид:

где - количество облигаций -того вида;

- цена приобретения облигаций/'-того вида;

- платежи в момент 7^;

- дисконтный множитель по ставке i.

Средняя ставка помещения (как показатель средней доходности) может быть

приближенно определена из ставок помещения каждого вида облигаций, и качестве

весов можно использовать стоимость облигаций по ценам приобретения.

I = S ijQjPj : S QjPj (2.37)

Существует и другой метод взвешивании. В качестве весов исполь­зуется

произведение показателей изменчивости на стоимость приобрете­ния облигаций,

т.е.

I = S ij Dj QjPj : S DjQjPj (2.38)

Пример 2.9. В таблице приведены данные портфеля облигаций с со­ответствующими

параметрами.

Рассчитать доходность этого портфеля облигаций.

Предварительно рассчитанные ставки помещения и показатели изменчивости

облигаций данного портфеля равны:

Ia = 7,44 Da = 6,0

Iб = 8,0 Dб= 3,5644

Iв = 10.88 Dб = 5,5163

Тогда средняя ставка помещения портфеля по (2.15) составит:

а по 2.16

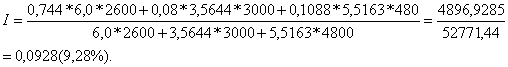
Для портфеля облигаций, как и для отдельного вида облигаций, целесообразно

рассчитать показатель изменчивости, который может охарактеризовать влияние

изменения рыночной процентной ставки на цену облигации, составляющих

портфель.

Изменчивость портфеля облигаций определяется как средняя ве­личина:

-

D= S ij Dj QjPj : S DjQjPj (3.39)

Пример 2.10. Используя данные примера (2.9), определить по­казатель

изменчивости портфеля облигаций

D = 5.0742 года

Рассмотрев методы определения доходности облигаций путем рас­чета ставки

помещения, определяемой исходя из рыночной цены обли­гации, перейдем к

решению обратной задачи - расчету цены облигации.

Облигации с периодической выплатой процентов без указания срока погашения.

Данный вид облигации является разновидностью веч­ной ренты, а оценку

облигации в этом случае можно свести к опреде­лению современной стоимости

этой ренты:

где R = QN - периодически выплачиваемый доход;

Q - процентная ставка, по которой выплачивается доход;

i - ставка помещения.

Расчетный курс такой облигации равен:

Рк = gN/iN * 100= g/i * 100 (2.40)

При выплате дохода несколько раз в году (Р раз):

Рк = gN/ P ((1+i)1/p-1) * 100 (2.41)

Рк = g/ P ((1+i)1/p-1) * 100 (2.42)

Пример 2.11. Облигация без срока погашения приносит 10 % ежегодного

дохода. Определить курс этой облигации, приняв ставку I помещения 12 %.

Но (2.19) находим:

Рк = 83.33

Если процентный доход выплачивается по полугодиям (Р = 2), то

Рк = 85.76

Облигации, проценты по которым выплачиваются в момент погашения.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13